Estimating average height of EUF students
Solving the exercise on terminology
1 Task
Consider the example from the previous task on estimating the average height of EUF students. Use the right vocabulary from sampling theory to describe it.
2 Possible solution
The population is the set of all students enrolled at the EUF (\(N=\) 6402). We are interested in the population parameter ‘average height’.
The sample is set of randomly drawn students from the population. We consider two cases, one with the sample size \(n=10\) and one with \(n=20\). We can assume the sample is a viable random sample, i.e. that it is unbiased and representative of the population.
The point estimate is the sample mean of the height, which is used to estimate the population parameter of interest (i.e. the average height of EUF students). This is viable since, given our assumptions, statements about the sample can be generalized to the population.
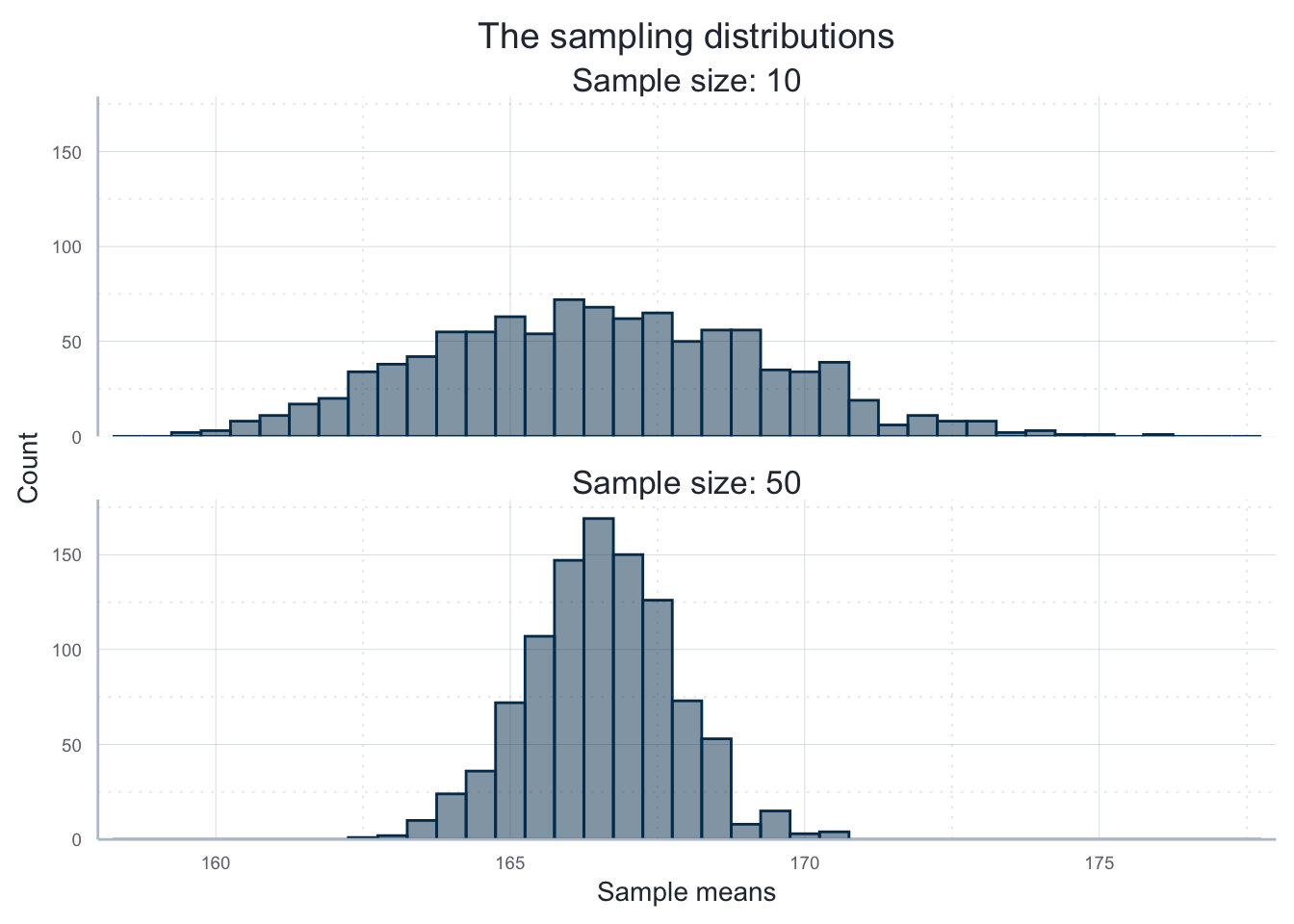
The sampling distribution visualizes the sampling variation, i.e. the variation of the point estimate obtained from different random samples. While in reality the sampling distribution remains unknown due to the fact that only one sample can be drawn, in the present case we used an artificial population and a Monte Carlo Simulation to characterize the sampling distribution as follows:
The standard error corresponds to the standard deviation of the sampling distributions and, due to the MCS framework, can be computed directly:
| Mean | Variation | |
|---|---|---|
| Sample size: 10 | 166.49 | 2.832 |
| Sample size: 50 | 166.54 | 1.244 |
3 Summary table
| Concept | Pendant in example |
|---|---|
| Population | Set of all students enrolled at the EUF |
| Sample | Set of randomly drawn students from the population |
| Sample size | Here 10 or 50 |
| Point estimate | Mean height of all students in the sample |
| Sampling distribution | The distribution of all the samples drawn from the population |
| Standard error | The standard deviation of the sampling distribution |
| Properties of the sample | We assume the sample to be a viable random sample, i.e. that it is unbiased and representative of the population, so its results are generalizable. |
| Census | This would mean to measure the height of every student in the population directly. |
| Inference | The strategy of understanding a population parameter by studying a sample and generalize to the population. |